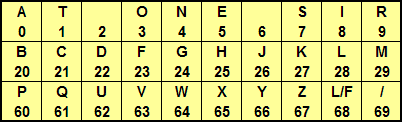
This page contains some examples of straddling checkerboards, a system to encode plain text into digits. This encoding is not a type of encryption and offers absolutely no cryptographic security whatsoever! The encoding only prepares the plaintext for the actual encryption process. Therefore, we call the result of encoding a plaincode, to stress that the message is still in its plain readable form. These checkerboards are easily designed from scratch or customized to fit the requirements of its users. This can range from simple text-only encoding to the use of special characters, words or codes for specific purposes or languages. The presented examples show the basic properties and possibilities of the checkerboard text-to-digit encoding. Anything is possible, as long as both sender and receiver agree upon a common system. The straddling checkerboard encodes the most frequently used letters into one-digit values. All other letters are encoded into two-digit values. This reduces the size of the message considerably (approx 1.5 digit/letter ratio against 2.0 for fixed two-digit systems). A checkerboard also breaks up individual letters into separate parts. This is called fractionation. Moreover, it does this irregularly (some are single and some double-digit values). When the checkerboard encoding is followed by an encryption algorithm that transposes the plaincode digits, then the irregular fractionation will cause the characters to be torn apart in a most irregular fashion and produce a far more complex encryption. Often, such encryption methods also use a checkerboard that has the order of its letters or digits scrambled to increase the total strength of the encryption. Note that the fractionation properties and scrambled letters or digits are irrelevant when the checkerboard encoding is followed by one-time pad encryption, as this type of encryption is unbreakable anyway. Here, only the checkerboard's efficiency matters. Please visit the one-time pad page for more information about the use of checkerboards for one-time pad encryption. A basic checkerboard, letter-optimized for English and based on the "AT ONE SIR" mnemonic, a table easily composed and written out on paper.
The table speaks for itself. "F/L" (68) is used to switch to figures and back to letters. Numbers are usually written out three times to exclude errors. The text "A54H" will therefore encode into "0 68 555 444 68 25". The field "/" (69) is used to separate letters or sentences. We can change the order of the top row letters to any desired combination. Some other anagrams for the "AT-ONE-SIR" top row letters are "SENORITA--" are "A-NOTE-SIR", "NATO-RISE-", "RAT-NOISE-", or "NO-TEA-SIR". If we change the position of the two
blank fields in the top row, then we also need to replace
the digit labels for the second and third row with the
digits that correspond to the top row empty cells. We can
also replace the top row letters by to the most
frequently used letters of another language. These can
vary quite a bit depending on the language. For more
details, visit the Wikipedia letter frequency
page Let's give a short example of how the checkerboard works by encoding the text "CONTACT JOHN AT 1830H". The top row letters are encoded into a single-digit value by taking the digit above the letter. The other letters are encoded in a two-digit value by taking the row digit, followed by the column digit. Once encoded into digits, we can encrypt the message with any digits-based encryption algorithm.
When decoding the message back from digits into text, we can easily distinguish single-digit from double-digit combinations. If the first next digit represents a letter in the top row, we have a single-digit value and simply take the letter underneath that digit. However, if the digit is located on the left-hand side of a row then we have encountered the first part of a double-digit value and must take the intersection of that digit's row and the following digit's column to find the letter that corresponds to that double-digit value. Although the checkerboard from above is simple to compose and to use, you can format such a table in another more practical and faster format for complex checkerboards with a larger number of cells:
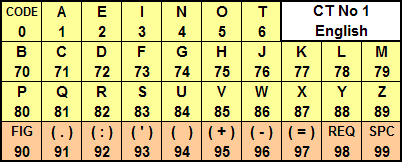
The following standard checkerboard is also optimized for English and has some extra features. Note that each additional empty cell in the top row enables the creation of an additional row with 10 new characters.
This checkerboard incorporates several punctuations and the space "SPC" (99). Here, "FIG" (90) has the same function as the "L/F" field from the previous table. The "REQ" (98) field is the abbreviation of "REQUEST" as in "request help" or "request new supplies". The table also contains a "CODE" field. This "CODE" prefix is used in combination with an additional codebook. Such codebooks contain all kinds of words, expressions or standard sentences, represented by a three-figure or four-figure code, depending on the codebook that is used. If, for example, "245" represents "Request more information" in the codebook, this would be encoded into "0245". Always use the "CODE" prefix (in this example "0") as prefix just before the actual code. When the receiver encounters the "CODE" prefix, he knows that he must decode the following three digits with the proper codebook into a word or phrase. The use of a codebook is optional but can reduce the message length considerably. The top row with most frequently used English letters for this checkerboard is memorized by the words "ON A TIE" in alphabetic order. We can optimize this checkerboard for French by using, in alphabetic order, the letters from the word "SAINTE". For German this would be "ANREIS "and for Spanish "SENORA". This, of course, requires a different completion of the second and third row with the remaining letters. The following checkerboard, also optimized for English, includes the most common English digraphs. This again reduces the required digits for certain words.
The CT-37 table is another extended version of the straddling checkerboard that includes additional characters. The table is easy to remember. It uses the 7 most frequent English letters "ESTONIA" in the top row. The two following rows are the remaining letters, completed with the "FIG" (89) field. The fourth row contains the "SPACE" (90) and "CODE" (99) field with the punctuation marks between them (less critical to remember).
The CT-37-Words table uses a mix of letters, words and code. "CODE" (6) is a shortened prefix for fixed length codes. The commonly used words "acknowledge", "request", "message", "rendezvous point", "grid" (coordinates), "send" and "supply" are represented by a small two-digit code. Omitting one more top-row letter or the CODE field will give another full row which could held 10 more words, expressions or short sentences (CODE could be added to this new row). This approach can reduce the message length enormously if the set of two-digit expressions is selected carefully.
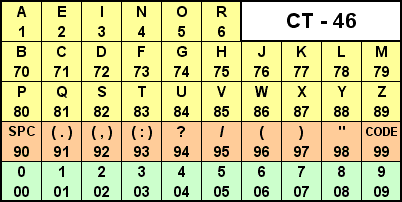
In the CT-46 encoding table, we can use four full rows since we have four unused digits in the top row. This encoding table is not that hard to memorize. In the first row the 6 most frequent letters AEINOR get the single digits. Each next row starts with the remaining digits 7, 8, 9 or 0. The second and third row are the remaining letters of the alphabet. The fourth row contains the "SPC"(90) and "CODE" (99) with the signs in between (less important to memorize). The fifth row are simply the numbers preceded by a zero.
The CT-55 table has even more additional characters. "L/F" (89) is used to switch from Letters (yellow) to Figures (green) and from Figures to Letters. This enables more characters with the same encoding value. The Red fields can be used in both Letters and Figures mode, thus a space, period, etc in a text doesn't require switching to Figures. Numbers are represented by its double code to exclude digit errors. An example: "F-16B" is encoded into 73 89 84 11 66 89 70. "CODE" (91) is again used as a prefix for four-digit codes and "RPT" (92) is used to repeat important pieces of text. This encoding table has the 7 most frequent letters, optimized for English, and is suitable for text with more figures and signs.
Of course, there are many other ways to encode characters into digits. The system of encoding characters into digits doesn't need to be scrambled or secure in any way when one-time pad encryption provides the security. Any method to encode into digits is good, as long as it is practical, doesn't make the message too long and isn't prone to critical errors. The shown examples are easily adapted to anyone's specific purposes. As explained before, checkerboards that are used in combination with an encryption method, other than one-time pad, preferably contain a scrambled alphabet or digits. This will strengthen the subsequent encryption considerably. Note that there are far more possible ways to scramble the alphabet than to scramble 10 digits. Therefore, we will focus on creating keyword based scrambled alphabets that include optimized letter frequency for a given language. Our first example uses two keywords and a double transposition. Let's use the keywords "OVERTURE" and "INTERGALACTIC". A first matrix is created with the first keyword and filled with the normal alphabet. A second, for now empty matrix, is created with the second keyword. The letters of both keywords are numbered according to their order in the alphabet. For letters that occur more than once we assign the lowest number to the most-left letter. Read off the letters of the first matrix, column by column, as determined by the first keyword order, and fill the second matrix, row by row, with those letters.
Next, read off and write down the letters from the second matrix, column by column, in the order as determined by the second keyword, and mark all most-frequent English letters, as provided by the mnemonic "AT ONE SIR".
Finally, the checkerboard is filled with the scrambled letters, the marked most-frequent letters in the top row, followed by the remaining letters. If we use the "AT-ONE-SIR" checkerboard from the first example on this page, the result is as follows:
The second example uses two keywords and a single transposition. Let's again take the keywords "OVERTURE" and "INTERGALACTIC". Write out the letters of the first keyword and number them according to their order in the alphabet. Also here, letters that occur more than once have the lowest number assigned to the most-left letter. Next, the matrix is filled with the second key word, without repeating any of the letters from that keyword. Complete the matrix with the remaining letters of the alphabet.
Read off the letters in the matrix, column by column, in the order as determined by the first keyword and mark all most-frequent English letters "AT ONE SIR".
Finally, the checkerboard is filled with the marked frequent letters first, followed by the remaining letter in the "AT-ONE-SIR" checkerboard:
Notice the completely different alphabets, created with the same two keywords but another transposition method. Although both methods create an excellent mix, it should be noted that the double transposition with two matrices creates the superior mix. Of course, these scrambled alphabets are useable for various differently formatted checkerboards, and we could even fill the matrices with a mix of letters, digits, codes or punctuations. On its own, these scrambled checkerboards constitute a monoalphabetic cipher, somewhat complicated by the irregular fractionation of the single- and double-digit combinations. This however will not provide any serious protection against basic cryptanalysis, even by a novice codebreaker. Its real potential is only fully exploited when a text, encoded with a scrambled checkerboard, is followed by a double transposition of the plaincode digits. A final increase of complexity is achieved when one or both transpositions are disrupted. This combination creates one of the most powerful manual ciphers that exist. This is due to the suppression of high frequency letters in combination with the highly irregular fractionation of the digit combinations by the two transpositions. Note that the matrices of the subsequent double transposition should preferably be unequal in width, one of even and one of odd width, and at least 15 to 20 columns wide. Remember, it's not required to scramble a checkerboard when the encoded message is followed by one-time pad encryption, as this type of encryption provides absolute security on its own.
Additional information Offsite
(opens in new tab)
|