What is Secret Splitting
The first type required all shares to retrieve the original information. The information, obtained from separate shares does not reveal any information or partial information about the original and does not assist in any way in retrieving the original information. It is mathematically impossible to obtain the original information if one of the shares is not available. The shares are information theoretically secure, read unbreakable. The second type requires less shares than the total number of shares to retrieve the original information. The security of this system depends on mathematical complexity to prevent disclosure of the original information and does not guarantee information theoretical security. Of course, you cannot simple cut a code or password in half or quarters, as this would reveal at least part of the code and provide clues to find the rest of the code or reduce the number of combinations to try out. A this page we discuss the secret splitting that requires all shares, which is information theoretical secure. Where to use Secret Splitting Secret splitting is especially useful in situations where you feel uncomfortable in sharing a secret with others and you have doubts about the reliability of some of them. You don't want one of them to misuse the secret behind the other's back. A person might be entitled to have the secret information but that doesn't mean you trust him to have full control over it. With secret splitting, misuse or unauthorized disclosure of the secret is impossible if there's at least one reliable person among the shareholders. And what's really great, more people with shares means more security, because more people have to agree on putting the shares together. That's just the opposite of sharing the secret itself, where more people means more risk. This is interesting when one person delegates responsibility over a secret code to several persons in specific situations. A parent can store his money, documents or valuables in a safe and split the number combination to the safe. All children receive a share and in case of emergency or death of the parent they can only access the safe when all of them agree upon opening the safe. None of them can act alone and get his hands on the money or documents. Each shareholder can even split his own share again into two shares, to hide his sub-shares separately as backup or destroy his original share and place his sub-shares at different places to increase security. Another possible application for secret splitting is the protection of secret passwords to access confidential computer data, encrypted files, a digital lock to a room, disable or enable an alarm system or to start or stop a device. This can range from a common computer login password to a nuclear missile launch code, where at least two people must agree upon entering the code to push the Big Red Button. You can also use secret splitting for secure remote delegation through insecure channels. Create a share for yourself and for one or more other persons. This way, you can be on the other side of the world and send your share to all other shareholders to give them access to a safe or encrypted computer file, to name a few. The shareholders can only retrieve the code at the moment that you decide to give them your share and they all need to agree. You can use any insecure method like e-mail, chat or telephone to send your share, because that single share never reveals any useful information to an eavesdropper. Secret splitting can also be useful to reduce the risk of interception during the transmission of codes, keys or other data. One could for example send a code through different media to the recipient. A code, split into four shares, could be send by insecure e-mail, post, SMS on mobile phone and by telephone, and all of these shares on different moments in time. An eavesdropper would have to continuously monitor and intercept all these communications at the same time , requiring vast SIGINT-like resources. If the eavesdropper misses only one share it will be impossible to reconstruct the original code. It is important to understand that
after the shares of two or more persons have been
combined, you should always set a new secret code
or password to your safe or computer, and create a
completely new set of shares, because your secret is
disclosed. You need a new secret code to avoid
unauthorized use of the old code. Types of Splitting or Sharing There are two main types of secret
splitting. The manual method, used on this page, requires
all shares in order to retrieve the secret information.
The threshold (number of required shares) is equal to the
number of shares. This is denoted as t = n. The advantage
is that you have an information theoretical secure
scheme. It's mathematically impossible to disclose the
secret if not all shares are available. This however will
cause problems when one share is lost, unless you have a
backup. Another advantage of this basic scheme, based on one-time pad encryption, is that it can be performed with
pencil and paper. You can download the Secure Code Splitter If you want to enable the reconstruction of the secret with fewer shares than the total number of shares, you will have to work with subsets. If, for example, Alice, Bob and John have shares, but two of them should be sufficient to retrieve the secret, you will need 3 different subsets (combinations of people) of 2 shares: Alice-Bob, Alice-John and Bob-John. Of course, each subset requires its own random shares. The downside of subsets is that this quickly becomes impractical when the number of participating persons increases. For 3 out of 5 shares you need 10 subsets and for 3 out of 6 you already need 19 subsets. Therefore, this scheme is only suitable for a single set or a limited number of subsets. Secret Sharing with threshold allows the reconstruction of shares with a fixed number of shares, less than the total number of shares, denoted as t < n.. You don't need subsets and each person receives a single share. If, for example, you have 5 shares with a threshold of 3, you will be able to retrieve the secret information with only 3 shares. Any 3 persons of a group of 5 can decide to disclose the secret. In contrast to secret splitting, the loss of one or more shares will not make reconstruction impossible, as long as at least the threshold number of shares remains. The threshold sharing schemes are either based on polynomial interpolation (Adi Shamir) or hyperplanes (George Blake). Unfortunately, these schemes required more complex calculations and are not suitable for use with pencil and paper. How does Secret Splitting work The basic secret splitting (t = n) we use is based on the principle of one-time pad encryption and all calculations are performed modulo 10 (addition without carry and subtraction without borrowing). The secret code is encrypted with one or more truly random keys and, in contrast to sending the encrypted secret to the receiver, we use the random keys and the encrypted code as shares. Only one-time pad offers the absolute security, required to create the individual shares. All calculations can be done by hand and secret splitting is therefore easy to apply by everyone without special knowledge of cryptography. Let us show the principle in a little example: Charlie splits the secret number combination 21 46 03 88 from his safe. A random key is subtracted digit by digit, without carry, from the number combination (e.g. 3 - 7 = 13 - 7 = 6). Alice and Bob each receive one share of the information from Charlie.
Alice's share contains truly random digits. Bob's share is Alice's share, subtracted without borrowing from the secret password, which produces a truly random result. Therefore, each of the shares on its own holds no information whatsoever that could help to retrieve Charlie's secret combination. This method is therefore information theoretically secure, read unbreakable, as long as the shares are kept separated. Retrieving the original combination is done by simply adding the two shares, digits by digit, without carry (e.g.. 7 + 4 = 1 and not 11).
For each additional share we must create an additional random key. If the secret information is to be split into 5 shares, we need 4 random shares and one result share. In such case, all random shares must be subtracted from the original information. Let's give an example to split the secret value 2 in four shares. We create three random shares with the values 5, 9 and 3. The result share will be 2 - 5 - 9 - 3 = 5 because (1)2 - 5 = 7 and (1)7 - 9 = 8 and 8 - 3 = 5. The four shares are therefore 5, 9, 3 and 5. To retrieve the secret we take 5 + 9 + 3 + 5 = (2)2 We can also split text. First, we need to convert the text into numbers. This is done by assigning a number to each letter. We can use the numbers 01 to 26 for the letters A to Z, 30 to 39 for the digits 0 to 9 and 00 for a space, or any other simple conversion system that suits your requirements. The method of splitting does not require the letter-to-number conversion table to be secret. The text can be a password, instructions or even a complete text.
To retrieve the secret information we simply add the shares together, again without carry, and convert the numbers back into letters. Splitting Computer Data We can also apply secret splitting on computer data. To split any type of computer file we first have to generate a random share with the same size as the file. This random file will be the first share. The second share is created by XOR-ing the original file and the random file. To retrieve the original file, the shares are XOR-ed. In the next example one byte is split into two shares.
We can also split data in more than two shares. For each new share we add another series of random bits and XOR them with the other shares.
The software that applies secret splitting should run on a secure computer and may not leave any traces after processing the shares. This includes secure deleting of the original file (not the normal delete function of your system, which doesn't actually delete the file). The secret splitting software should meet the same standards as quality encryption software regarding memory storage, secure file processing and generating quality random numbers (see requirements randomness in next section). Also, the shares should be stored securely on external media or, less advisable, other computers. Keeping Secret Splitting secure The secret splitting we used on this page is based on the principle of one-time pad encryption and all calculations are performed modulo 10 (addition without carry and subtraction without borrowing). The secret code is encrypted with one or more truly random keys and, in contrast to sending the encrypted secret to the receiver, we use the random keys and the encrypted code as shares. However, there are two important rules to obtain absolute security.
Never simply use normal six-sided dice by adding the value of the dice and discarding two values. This method is statistically unsuitable to produce values from 0 to 9 and thus absolutely insecure (the total of 7 will occur about 6 times more that the values 2 or 12). Instead, use one black and one white die and assign a value to each of the 36 combinations, taking in account the order and color of the dice (see table below). This way, each combination has a .0277 probability (1 on 36). We can produce three series of values between 0 and 9. The remaining 6 combinations (with a black 6) are simply disregarded, which doesn't affect the probability of the other combinations.
Another method is a lotto system with balls, numbered from 0 to 9. After extracting a number, that ball must be mixed again with the other balls before extracting the next number. Such methods are suitable for small amounts of random numbers, for instance splitting keys or passwords. If a large quantity of numbers is required, for instance to split computer files, the best solution is to purchase a hardware based PC card with random noise source. Note that the default computer RND function does not produce true randomness!
One possible way to store an individual share is a small sealed - glued - plastic container that needs to be broken in order to get access to the share (wrap the folded text in aluminium foil). Seals can be glued into the transparent container. A damaged container and thus compromised share would be noticed immediately. Of course, the plastic container must always be stored on a physically secure place. The owner could always perform a security verification and demand the shareholders to show their undamaged share. This is comparable with the famous so-called biscuits that are broken to obtain nuclear codes. The system will be information theoretically secure if the rules of randomness and physical separation are applied correctly. It is mathematically proven that there's no way to retrieve the secret information, other than getting your hands on all required shares. Of course, if you have split the code of a cheap five dollar lock, you will have five-dollar-security. It's useless to protect the key code of a safe if a simple crowbar can open it. On the other hand, if you split the combination of a safe deposit box in your bank, you can be sure that no individual shareholders can access that safe. Obviously, after the shares have been combined to obtain the secret code, you should always set a new secret code or password to your safe, computer or whatever, and create a completely new set of shares to avoid unauthorized use of the old code or secret.. Finally, the method as presented on this page had another very important property. Since this system is unbreakable, the loss of one share will always result in the definite loss of the secret information, unless the shareholders have a copy of the original. Also, be sure to double-check the shares you created if you intend to destroy the original! There's no way back if a share is lost or destroyed by accident! It might be useful that the shareholders have one extra copy of their share on another secure location. Any shareholders could also decide to split his own share into two sub-shares and place them at different locations as a secure backup. More on the website
Further Information (offsite, opens in new tab)
|
 Secret splitting, also called secret sharing,
enables you to split a secret into different shares and
give these share in the custody of multiple persons
without disclosing the secret itself. The expressions
splitting and sharing are a bit misleading as we don't
split the secret but compute the shares and we don't
share the secret itself but rather share the
responsibility over the secret. There are two types of
splitting.
Secret splitting, also called secret sharing,
enables you to split a secret into different shares and
give these share in the custody of multiple persons
without disclosing the secret itself. The expressions
splitting and sharing are a bit misleading as we don't
split the secret but compute the shares and we don't
share the secret itself but rather share the
responsibility over the secret. There are two types of
splitting. The first rule is that the random keys (read
shares) must be truly random, just as
with one-time pad encryption. To generate true
randomness, there are some practical solutions for small
amounts of random digits. You could use five ten-sided
dice (see right). With each throw, you have a new
five-digit group.
The first rule is that the random keys (read
shares) must be truly random, just as
with one-time pad encryption. To generate true
randomness, there are some practical solutions for small
amounts of random digits. You could use five ten-sided
dice (see right). With each throw, you have a new
five-digit group.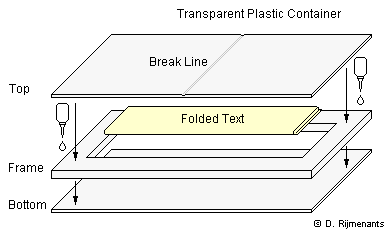 The second rule for
absolute secure splitting is of course the physical
separation of the individual shares. At least
one of the shares should never be accessible to the other
shareholders. The shares must always be protected in such
way that a compromised share would be noticed.
The second rule for
absolute secure splitting is of course the physical
separation of the individual shares. At least
one of the shares should never be accessible to the other
shareholders. The shares must always be protected in such
way that a compromised share would be noticed.